Modelling

A Dynamical Model of Immune-System Response to mRNA, Live Virus, and Inactivated Vaccines

By

Note: This post was originally a short technical article I shared on the Wolfram Community forums. For an interactive experience with live demonstrations or to download this text and source source code as a Wolfram Notebook, please visit the original post here. 

Source article: Zhaobin Xu, Jian Song, Hongmei Zhang, Zhenlin Wei, Dongqing Wei, Jacques Demongeot, A Mathematical Model Simulating the Adaptive Immune Response in Various Vaccines and Vaccination Strategies, medRxiv 2023.10.05.23296578. DOI: https://doi.org/10.1101/2023.10.05.23296578

Introduction:

The accomplishments of vaccination are numerous, leading to significant advances in human health. Yet new infectious diseases and evolving pathogens constantly challenge our understanding of vaccine efficacy and immunity. Mathematical modelling is a crucial lens through which we can reach a more comprehensive understanding of these complexities. By simulating the biological responses to vaccines, models can provide critical insights into disease progression, vaccine performance, and optimal strategies for developing vaccines.

 
In this short text, we’ll explore an approach to constructing one such model in the Wolfram Language. We will reproduce a compartmental dynamical model of adaptive immune responses to vaccine treatments described in a recent preprint from medRxiv.org: A Mathematical Model Simulating the Adaptive Immune Response in Various Vaccines and Vaccination Strategies (Xu et al. 2023). Compartmental models are a class of mathematical models which divide variables of interest into sections or “compartments”. Each compartment represents a specific state within the system being studied. The models track how entities, like cells or molecules, interact within and between these compartments over time.
 
The stated goal of the paper is to construct a novel mathematical model to quantitatively research the activation of adaptive immune responses by vaccines. This model is used to simulate and compare the dynamics of antibody levels after administering different types of vaccines (inactivated, attenuated live virus, mRNA), thereby contributing to a better understanding of the mechanisms of various vaccines and vaccination strategies. Through the model, the authors aim to suggest strategies for vaccine design, while providing a comprehensive portrait of the inducible interactions between antibodies and antigens in the immune process.

Setup

Dependencies

We will make use of the CompartmentalModelling paclet. You can install and load the paclet like so:

You can find documentation for this paclet by following this link.

Paper Tables

You can find the definitions for the tables of reactions, reaction variables, and reaction parameters in the original version of this post on Wolfram Community.

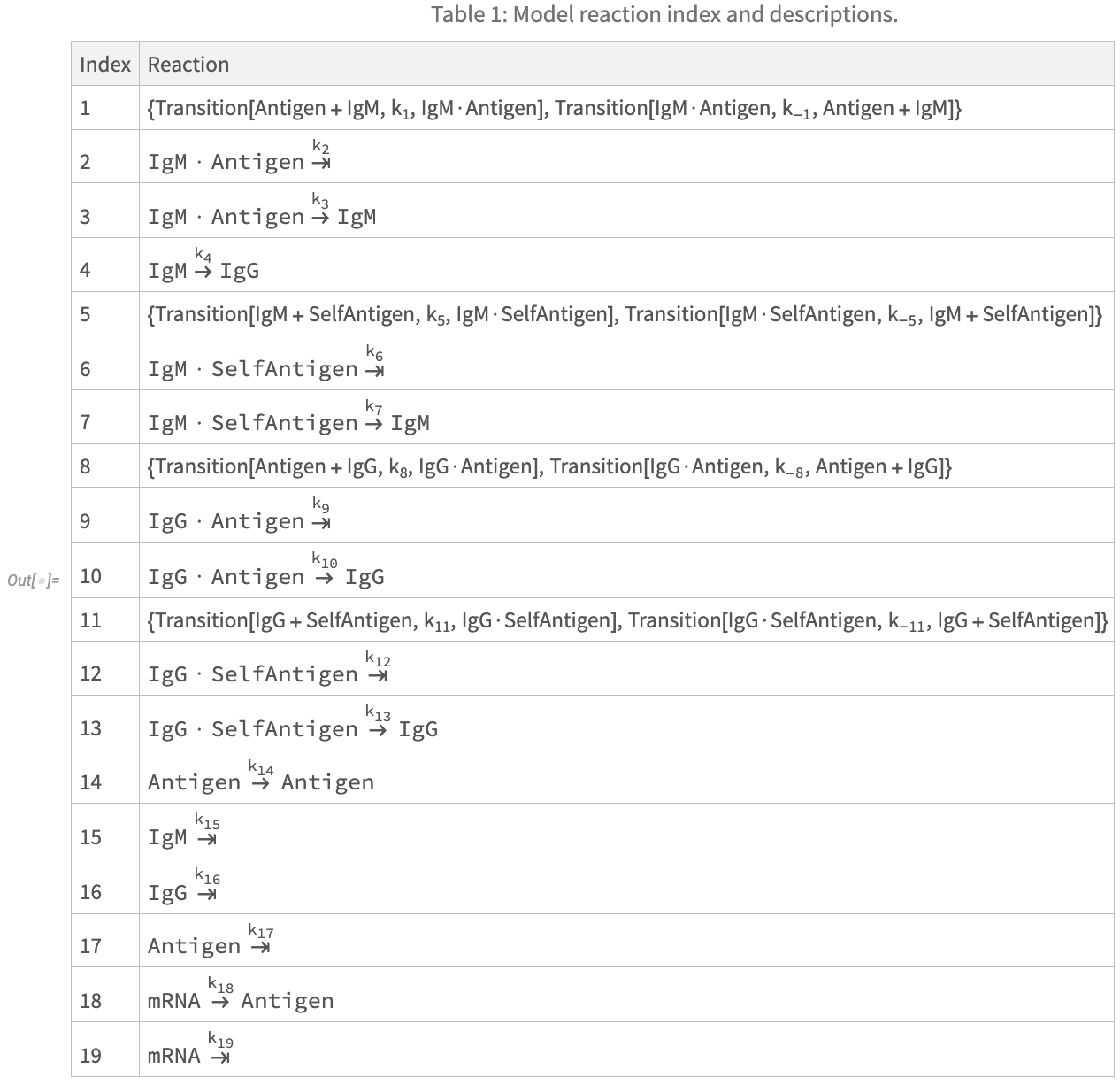
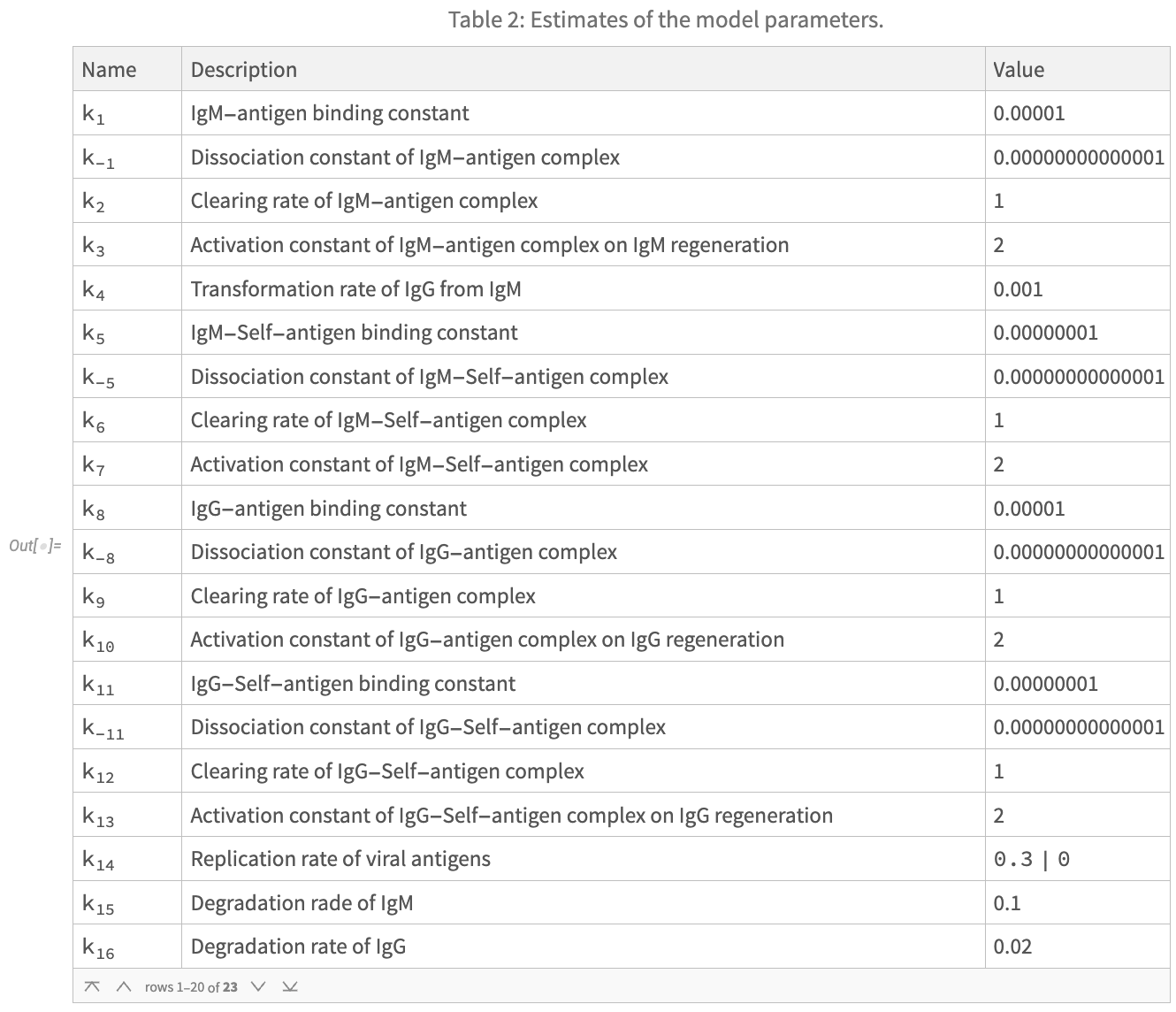
Reactions, Parameters, and State Variables of the Model

The authors of the paper helpfully provide three tables fully specifying the interactions between state variables (components) of the system, as well as model parameters and initial conditions. I have reproduced these tables below. Note that some parameter values and initial conditions depend on the selected vaccine treatment type. More precisely:

  • The replication rate of viral antigens, described by parameter k_14 should be set to .3 in the case of a simulation of an attenuated live virus vaccine, and 0 otherwise.
  • The initial condition of the state variable x_2 (Antigen) should be set to 10^6 for simulation with an inactivated vaccine, 0 with an mRNA vaccine, and 1 for an attenuated live virus vaccine.
  • The initial condition of the state variable x_9  (mRNA) should be set to 0 for simulation with an inactivated or attenuated live virus vaccine, and 10^6 for and mRNA vaccine.

For a more in depth explanation of these parameters and initial conditions, please refer to the paper.

Extracting Model Information

We can use tools from the CompartmentalModelling paclet to extract useful information about the model. For instance, we can use CompartmentalModelGraph from the CompartmentalModelling paclet to visualise the model’s structure:

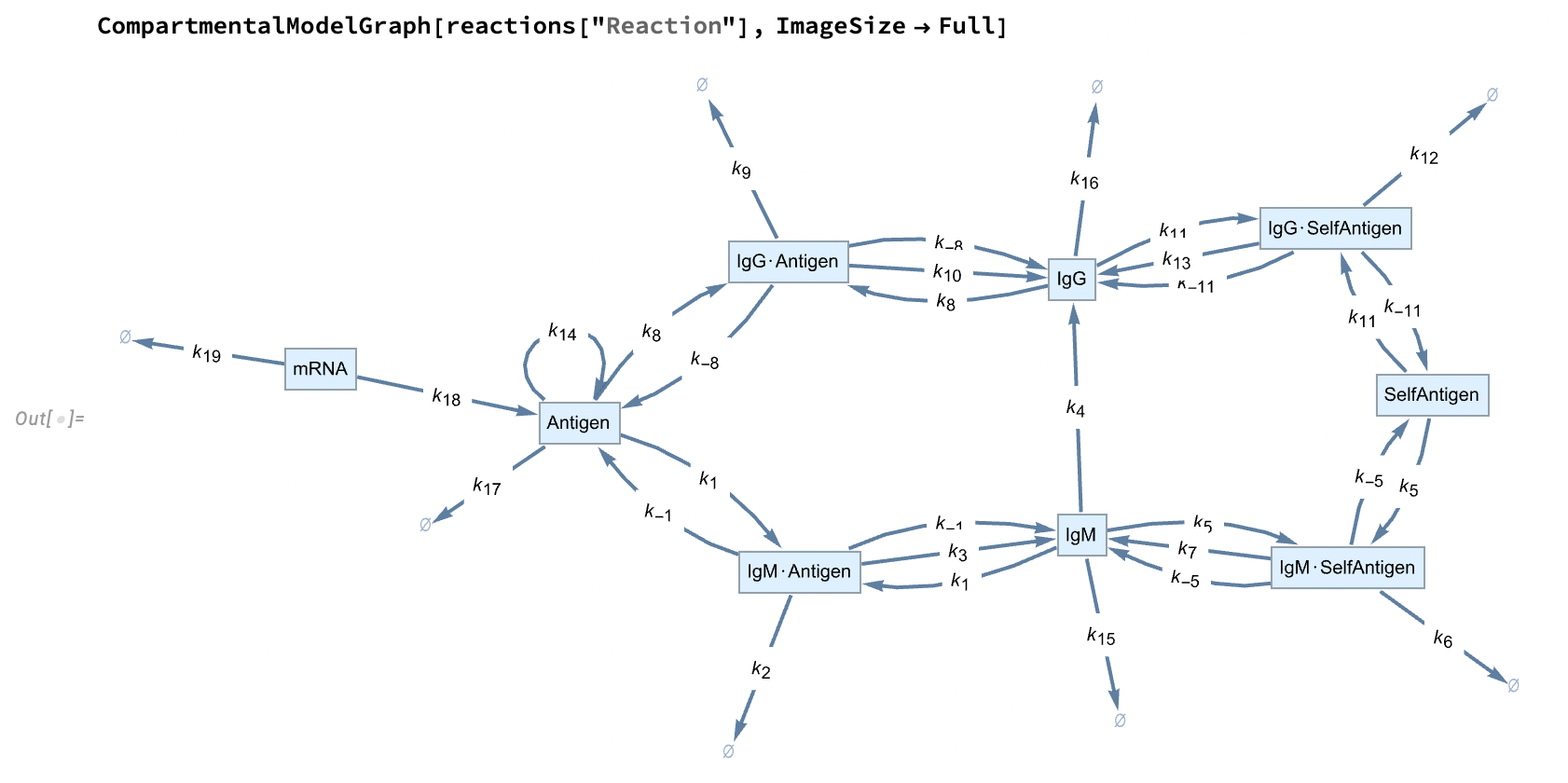
The CompartmentalModelling paclet contains convenient functions to streamline the process of building models. For instance, we can use KineticCompartmentalModel to generate differential equations for from a list of component transitions (the reactions).

Fetch the model data:

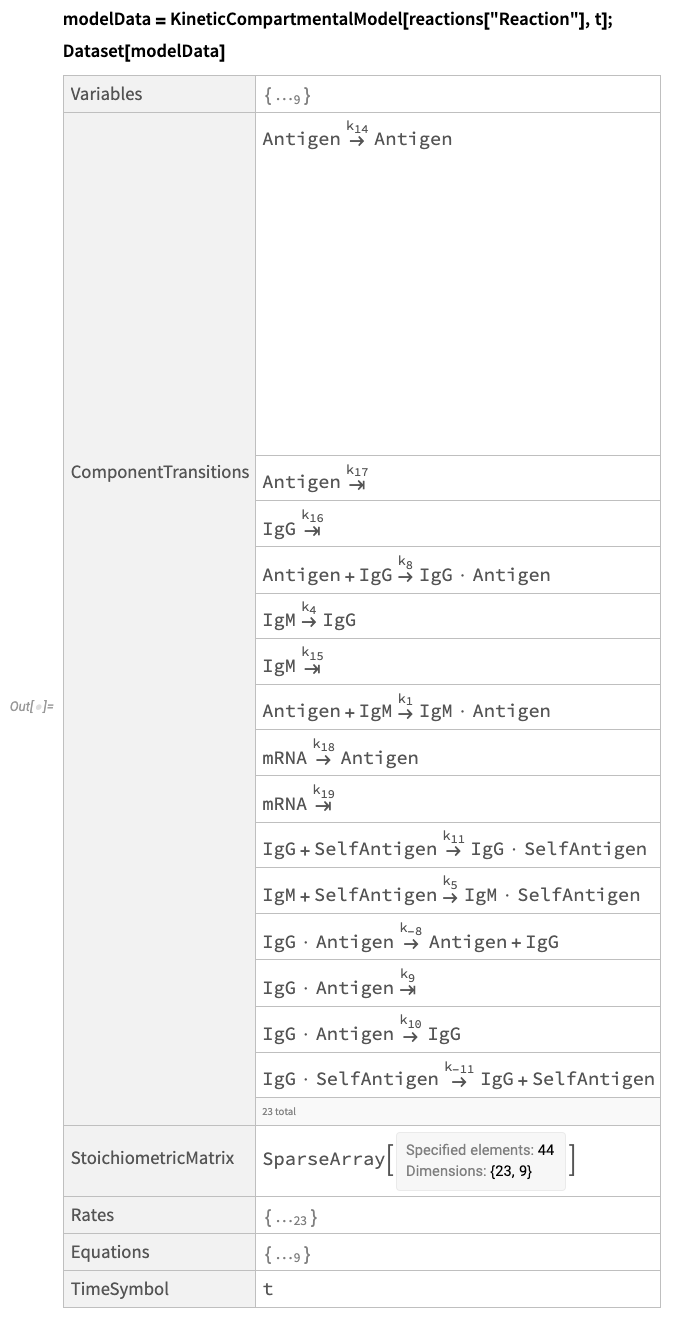
These data are very useful for quickly building and simulating compartmental models.

Numerical Simulations

Preparing Model ODEs

Owing to details related to the original code implementation of the model, the authors provide a slightly modified system of ODEs describing the model. This system is reproduced below and numerically approximated using NDSolve for different vaccine treatments:

Reproduce the ODEs from the paper:

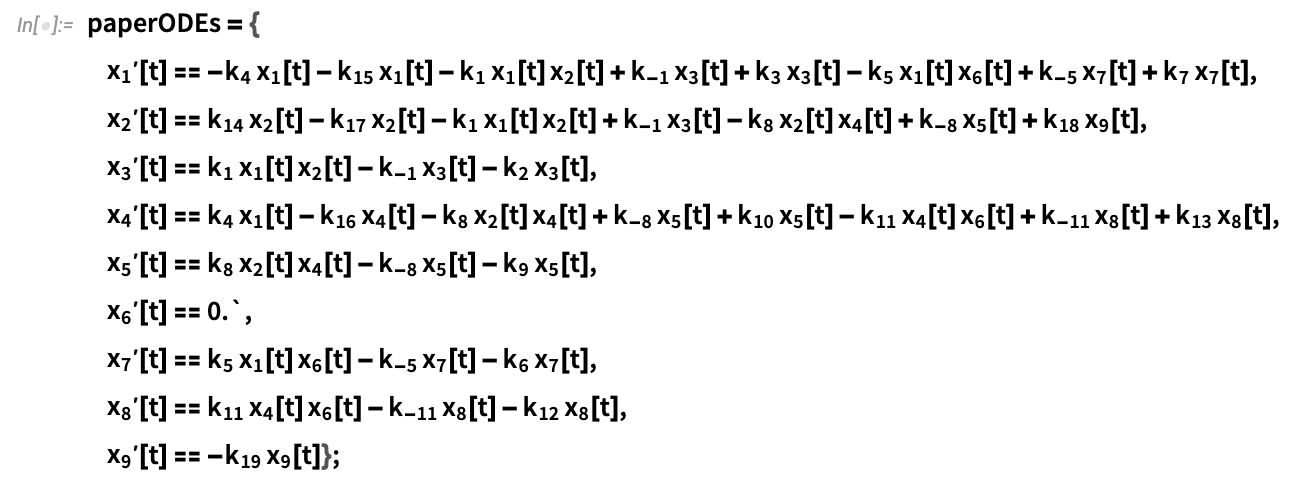
Let’s also get some replacement rules to easily convert between the variable names in plain English, and the symbols used in the paper for the model’s system of ODEs.

Plain English variables <--> ODE variables:

Vaccine Treatment Simulations

In the paper, the authors model three cases:

  1. Inactivated Vaccine Simulation
  2. Attenuated Live Virus Vaccine
  3. mRNA Vaccine

These cases are solved numerically in the three following sections. The inactivated vaccine and mRNA vaccines each take two injections, one at one at 

t=0, the other at t=50. The attenuated live-virus vaccine takes a single dose at t=0. The injection dosage is of 6^10 for all simulations.

1. Inactivated Vaccine Simulation

Model-specific parameters and initial conditions:

  • Replication rate of viral antigens: k_14=0
  • Antigen = x_2[0] = 10^6
  • mRNA = x_9[0] = 0

Define model parameters corresponding to the inactivated vaccine setup:

Define initial conditions of the system corresponding to the inactivated vaccine setup:

Construct the system of equations for NDSolve, with parameter values and initial conditions:

Solve numerically with NDSolve, from t=0 to t=100:

Plot the solution:

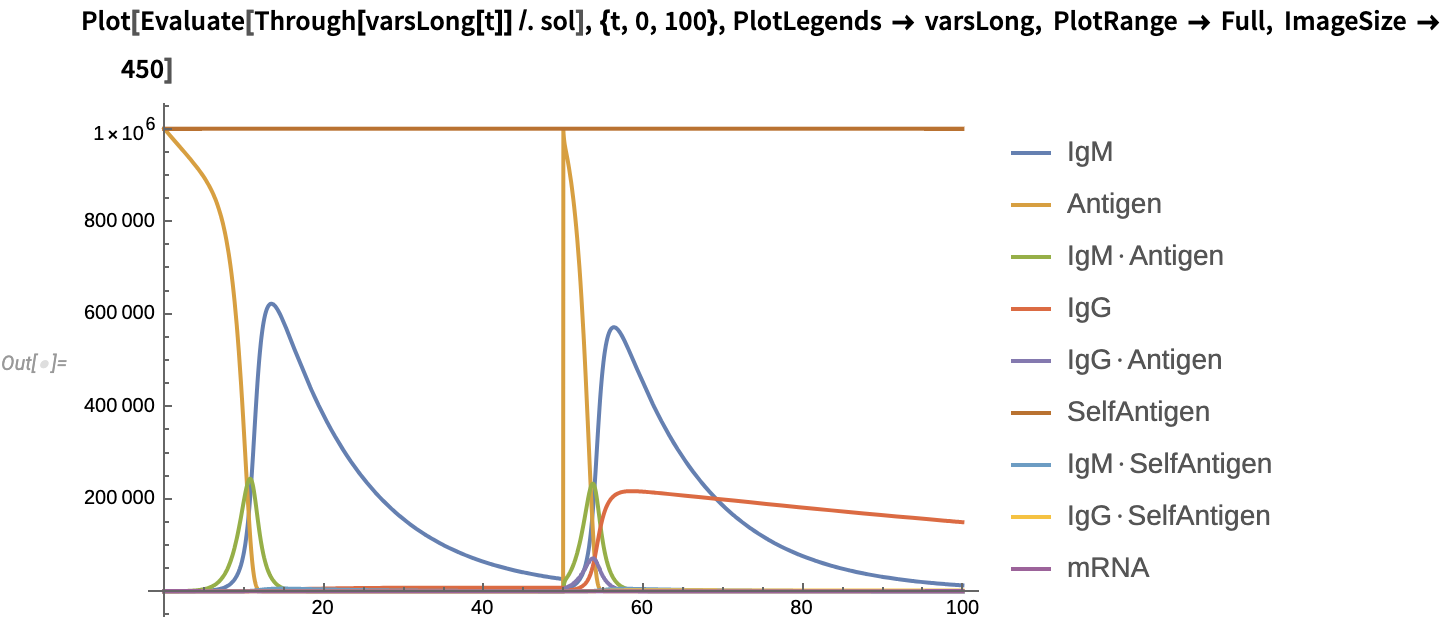
2. Attenuated Live Virus Vaccine

Model-specific parameters and initial conditions:

  • Replication rate of viral antigens: k_14=0.3
  • Antigen = x_2[0] = 1
  • mRNA = x_9[0] = 0

Define model parameters corresponding to the inactivated vaccine setup:

Define initial conditions of the system corresponding to the inactivated vaccine setup:

Construct the system of equations for NDSolve, with parameter values and initial conditions:

Solve numerically with NDSolve, from t=0 to t=100:

Plot the solution:

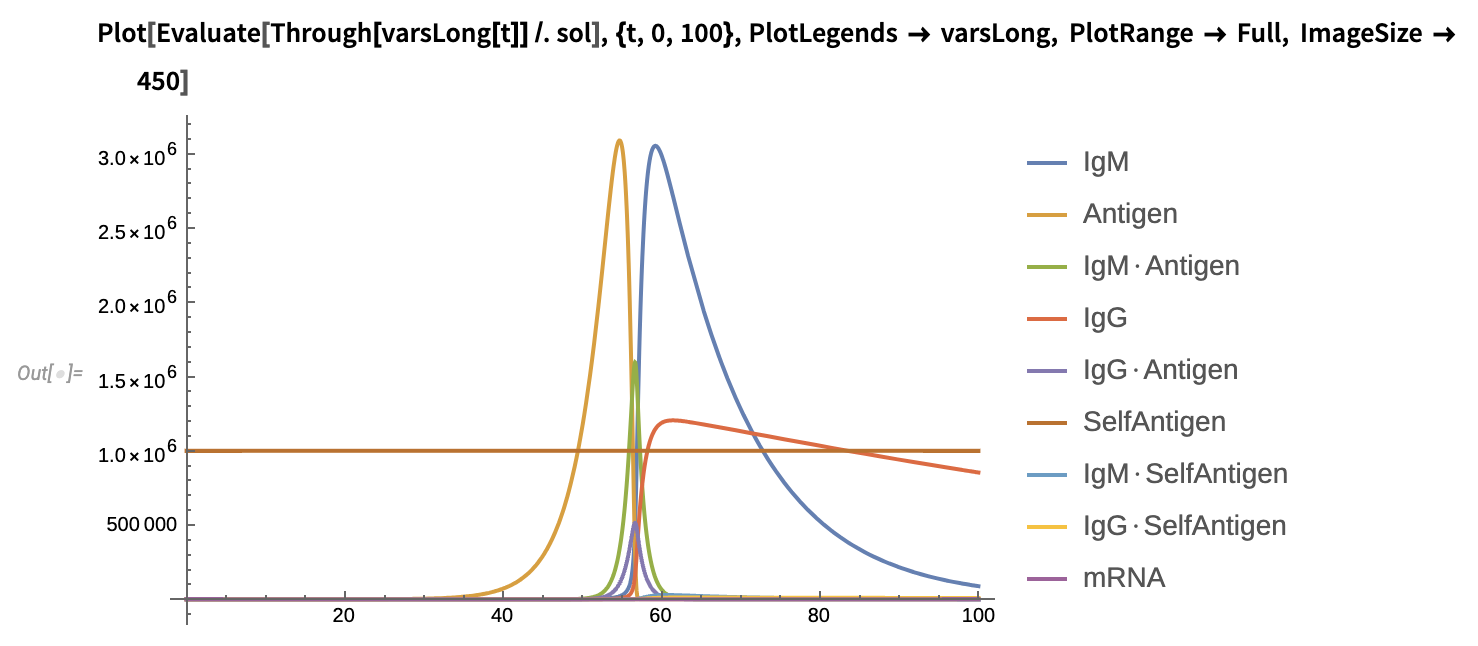
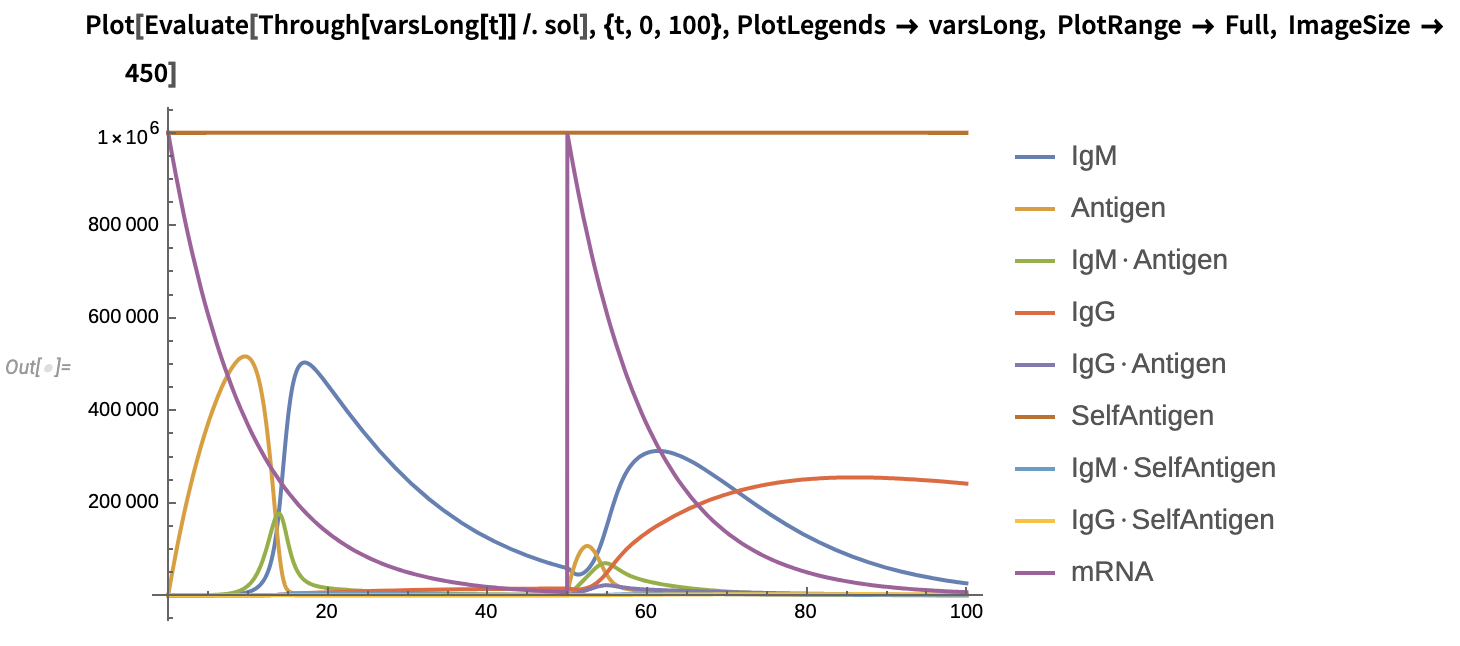
3. mRNA Vaccine

Model-specific parameters and initial conditions:

Replication rate of viral antigens: k_14=0
Antigen = x_2[0] = 0
mRNA = x_9[0] = 10^6

Define model parameters corresponding to the inactivated vaccine setup:

Define initial conditions of the system corresponding to the inactivated vaccine setup:

Construct the system of equations for NDSolve, with parameter values and initial conditions:

Solve numerically with NDSolve, from t=0 to t=100:

Plot the solution:

Closing Notes

 
Through the exploration of this dynamical immune response model, we have seen how mathematical modelling in the Wolfram Language, can be used to derive insights into complex biological systems.
 
If you are interested in this work, and would like to learn more, please make sure to give the source paper a read! I primarily intend this post to demonstrate how one might conduct this form of modelling in the Wolfram Language. I also highly encourage you to try Bob Nachbar’s CompartmentalModelling paclet. The CompartmentalModelling paclet is not just for biologists, but could be a valuable tool for anyone dealing with interconnected systems that can be represented as compartments. 

Related posts